Tuning up your display for optimal viewing of astronomical images
 |
Displaying in a proper and consistent way deep-sky astronomical images on a computer screen is not as straightforward as it seems, even with recent monitors. Much of the fine image details lie in the dark part of the images, whose brightness can hardly be pushed up without ruining the global visual impression, exacerbating the background noise, or overexposing bright regions. Depending on the screen model and the amount of ambient illumination, these dark parts may appear either washed out or totally black. |
Choosing the right LCD technology
 Dark shade fidelity is still LCD monitors’ Achilles heel. The rendering of the cheapest models, based on twisted nematics (TN) liquid crystal technology, varies particularly strongly with viewing angle and must be avoided for preparing astronomical image media. Unfortunately most laptops are equipped with TN panels. LCD monitors based on IPS, MVA and PVA technologies offer consistent rendering on much larger viewing angles, albeit being more expensive and more power-hungry.
Dark shade fidelity is still LCD monitors’ Achilles heel. The rendering of the cheapest models, based on twisted nematics (TN) liquid crystal technology, varies particularly strongly with viewing angle and must be avoided for preparing astronomical image media. Unfortunately most laptops are equipped with TN panels. LCD monitors based on IPS, MVA and PVA technologies offer consistent rendering on much larger viewing angles, albeit being more expensive and more power-hungry.
Gamma correction
Another issue is gamma correction. It is often forgotten that the true light intensity $I\,’$ (or more formally, radiant emittance) displayed by a properly adjusted display device is related to the pixel value $p$ stored in the computer’s frame buffer through the power law
| $$ I\,'(p) \propto p^\gamma, $$ | (1) |
where $\gamma$ is what is called the display “gamma”: this operation is sometimes called “gamma expansion”. It must be checked that the monitor gamma expansion is correct over the whole dynamic range, and more specifically for the dark shades. The display gamma for computer monitors is generally assumed to have a value of 2.2 nowadays, although in practice it may vary from about 2.0 to 2.5. This exponent between the video signal amplitude and the display light intensity comes from the times when Cathode-Ray Tubes (CRTs) were ruling the world of electronic imaging. For that matter, the inverse relation (“gamma compression”) applies to most electronic image and video storage formats, including old analog ones like Laserdiscs and video tapes. It also applies to the data stored in popular such as JPEG, PNG, and TIFF, and to signals transiting through video cables.
Calibrating the display
Many monitors, even recent ones, do not come properly calibrated by default. This is not a matter of gamma alone, and achieving a correct calibration normally requires a dedicated probe. But here in the context of astronomical imaging we will simply focus on contrast, brightness, and gamma adjustments.
If you want to check the gamma calibration of your display (monitor+video card), you must first make sure that a neutral transfer curve is selected in the monitor’s menu, and that the image sharpness settings are set to the most neutral position. . If your operating system supports ICC profiles, you might also want to install the ICC profile provided with your monitor (if it exists). ICC profiles are currently supported by the Safari v4+ and Firefox v3.5+ on the Windows and MacOS X platforms, and are especially important for screens with a colour gamut that differs significantly from that of the sRGB system. Note that in Firefox only graphics with colour management tags (overall a minority of all images on the web) are ICC-corrected by default. To apply your current system’s ICC profile to all images you might want to set gfx.color_management.mode to 1 in the about:config preference settings, as shown below (recommended only for displays with a native rendering not close to sRGB).
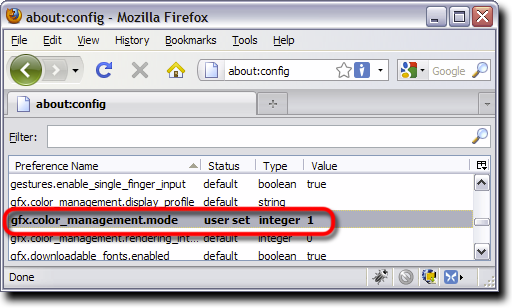
The next step consists of making sure that the monitor image controls are set appropriately, and that the extreme blacks and white levels are not clipped (see this test and this test). You are now ready to check on a gamma calibration pattern that your display gamma is close to the canonical value of 2.2. Other gamma check patterns can be found here or there. You may also create your own gamma calibration pattern yourself! Here is an example using MATLAB (and its Image Processing Toolbox):
h = 400;
g = 2.2;
[x,y] = meshgrid(1:w,1:h);
x = (x-1)/(w-1);
ymod = mod(y,2)*2–1;
y = (y-1)/(h-1);
ima = x;
ima(1:h/2,:) = 0.5*(1.0+ymod(1:h/2,:).*cosd(720.0*x(1:h/2,:))).*(y(1:h/2,:)*2).^2.0;
ima(h/2+1:h,:) = 1.0-ima(h/2:-1:1,:);
ima = ima.^(1/g);
colormap(gray)
imshow(ima,[]);
 |
The pattern consists of interleaved sine waves with opposite sign. The interleaving is perpendicular to the video scan lines to minimize analog signals. The sum of the sine and its opposite is constant for all x and therefore such a pattern displayed on a screen with the proper gamma (the recommended sRGB default $\gamma = 2.2$) should appear uniform along the horizontal axis, over the whole luminosity range:
Vertical bands will appear if the display gamma is too low:
… or if it is too high:
|
Some monitors offer a gamma adjustment, but the best way to correct the display gamma is at the graphic card level. Graphic card drivers generally come with a colour correction interface where a gamma adjustment slider is present.
Perceptual image reproduction and astronomical image encoding
In practice, it is important to consider two factors that have a significant impact on the perception of reproduced images :
 |
| Bartleson-Breneman effect: the series of squares on the right is identical to that on the left, but the perceived contrast between squares seems less because of the dark background. |
- Experimental studies have shown that the perceived “contrast” of an image is comparatively lower with a dim image surround compared to a bright surround (Bartleson & Breneman 1967): see illustration on the right. Now, contrary to real scenes or even printed images, images displayed on screens are usually watched in a relatively dim light environment; in such conditions a slightly exaggerated contrast will therefore result in a more natural-looking picture on a movie screen, a TV, or even a computer monitor.
- Screen glare/viewing flare: no screen displays a totally perfect black in typical viewing conditions. The amount of flare depends on the technology (set by the minimum monitor black level, or the maximum film density) and the environment (ambient light reflected on screen). The net effect of flare is to brighten the darkest areas of the displayed image.
Recognizing the significance of these two factors, engineers have designed gamma compression laws slightly more complex than the simple $I^{1/\gamma}$ that would suffice to compensate for the power-law gamma expansion of (1). In other words, compensating for flare and the Bartleson-Breneman effect is done at the encoding level. The gamma compression model used for the sRGB (World Wide Web) and the ITU-R BT Rec.709 (High Definition TV) international standards is
| $$p\,(I) = \left\{\begin{array}{ll}a.I & \mbox{if } 0 \le I \lt I_t\\&\\(1+b).I^{1/\gamma} – b & \mbox{if } I_t \le I \le 1\end{array} \right.$$ | (2) |
|
How do these perceptual corrections work with deep-sky astronomical images? Since deep sky images are mostly dark, and therefore operate in a different regime of the Bartleson-Breneman effect compared to “regular” images, we may wonder whether compensating simply for the standard 2.2 display gamma using $p(I) = I^{1/\gamma}$ is not the most appropriate choice. The answer depends on context and purpose. The sRGB curve, and even more notably the Rec.709 curve, have both a tendency to “bury” much of the dark tones of the image into a velvety black background. The figure below shows the same data encoded with three different gamma correction laws using STIFF 2.0. On a rather dark background like this page, and with low ambient lighting, we find sRGB-corrected images to provide the most visually-pleasing rendering of the data, with the linear part of the transfer curve helping to reduce the apparent contribution of noise. The power-law correction leads to slightly more washed out and noisy results, while the Rec.709 version looks excessively contrasty and wipes out the faintest galaxies. But when seen with a white surround (click on images) or a brighter ambient lighting, the power-law correction is the only one that keeps the faint details still well-visible, and becomes the best choice. The sRGB correction seems therefore to be more appropriate for illustration purposes when the image is to be displayed on a dark background, or when the sky is very “noisy”. The 0.45 power-law correction seems a better choice for brighter surrounds, display devices with a gamma higher than 2.2, or for scientific visualisation purposes where being able to see details in the background noise is important. |
 |
 |
 |
| 1/γ= 0.45 power law | sRGB | Rec. 709 |
Further reading
- H.-C. Lee 2005: Introduction to Color Imaging Science, Cambridge University Press
- M.C. Stone 2003: A Field Guide to Digital Color, A.K. Peters, Ltd
On the Web
- The STIFF homepage at AstrOmatic.net
- hardware.info monitor comparison page
- LCD monitor test page at lagom.nl
- Charles Poynton’s gamma FAQ
- Color context by S.Grais at DePaul University
- Modern color theory concepts and applications by B. MacEvoy at handprint.com








 with $\gamma = 2.4$, $a = 12.92$, $b = 0.055$, $I_t = 0.00304$
with $\gamma = 2.4$, $a = 12.92$, $b = 0.055$, $I_t = 0.00304$